to the contents
forward to playing
on several jew's harps
| + Tone Generation + Scale of the Jew's Harp: The Natural Harmonic Row + Resonances: Sounds and Pitches, Melodies and Accompaniment + Open and Closed Vocal Tract + Literature |
| back to playing techniques |
to the contents |
forward to playing |
 frequency analysis: Audacity
frequency analysis: Audacity 
 further
calculations and plotting of exported frequency data: Libreoffice-Calc
und -Draw
further
calculations and plotting of exported frequency data: Libreoffice-Calc
und -DrawThis chapter presents some background knowledge: It starts with tone generation and the specific
scale of each jew's harp, dependant on the tuning of the reed - the natural harmonic row. The sound of
playing is formed in the mouth and throat. These are the resonating
cavities also forming the sounds of speech.
Tone Generation
It is difficult to place the jew's harp in the system of musical
instruments. On the one hand it is classified as plucked idiophone,
together with the musical clocks: The plucked part of the instrument
sounds itself. On the other hand, the jew's harp belongs to the
aerophones, together with the wind instruments and the instruments of
the accordion type: In this class of instruments the sound is generated
by a vibrating air column (flutes etc.) or by a stream of air stimulated
to sound by a reed (harmonica, accordion). The affinity to the accordion
instruments becomes clear when jew's harps, hold against the lips and
teeth respectively, begin to sound without being plucked, just by
breathing in or out. Clemens Voigt of Dan Moi (see links)
told me how this effect works: The reed has to be shifted a little from
the level of the frame, and the air flow has to pull it back towards the
frame level (figure 1, cross section of a jew's harp).
figure 1
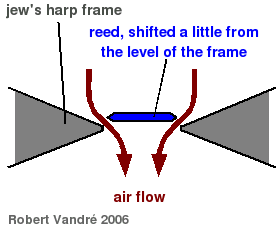
On bow-shaped jew's harps the effect works if the reed is pushed gently at the basis by the thumb of the hand holding the frame as in figure 1 to shift it a little. In this way the jew's harp works just like a harmonica. In sound example 14 (64 KB) the tone c is heard, first played on a harmonica, than plucked on the jew's harp, and finally stimulated by breathing in on the jew's harp.
|
Scale of the Jew's Harp: The Natural Harmonic Row |
In our common tonal system the octave consists of 12 equal half-tone
steps (enharmonic temperament). This means, that the number of
vibrations per second (frequency, unit: Hz) of one tone multiplied with
1,059463 equals the frequency of the following half tone. If any
frequency is multiplied again and again with this factor, after 12 steps
the frequency is just doubled, and the respective tone is transposed in
an octave above. Thus, as the frequency of successive half tones always
is altered by the same factor, the absolute difference of the
frequencies is less at deep tones (low frequencies) and higher at high
tones (high frequencies).
The tone row of the jew's harp (as well as that of any instrument with a
natural harmonic row) is different: The reed of every harp has
its specific fundamental frequency, e.g. 98 Hz (tone G) or 58.3 Hz (B1).
The vibration that produces the fundamental note is always accompanied
by its overtones. The overtones of a harmonic sound, like the one
produced by the jew's harp reed, are called partials or harmonics. They
have frequencies that are multiples of the fundamental frequency. Thus,
the jew's harp tuned G plays the multiplication tables from 98 Hz, the
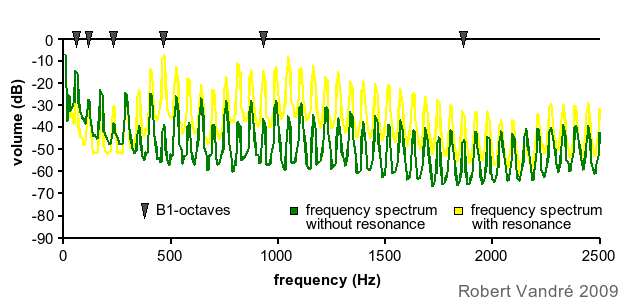
one tuned B1 that from 58.3 Hz. This can be seen in figure 2: The sound
of a jew's harp was recorded without contact to the mouth, that is,
without resonances of the oral cavity (sound
example 15a, 126 kB). The freeware programme Audacity was used to
determine the frequency spectrum. Each peak of the green curve is
one tone played by the jew's harp reed. They are situated at
regular intervalls of 58 Hz. The first peak on the left under the first
grey triangle is the fundamental note. The next, smaller peak to the
right is the first overtone or partial, the following higher peak is the
second partial and so on. The yellow curve shows a frequency spectrum of
the same jew's harp as played normally with contact to the mouth (sound
example 15b, 130 kB).
Note: Without resonance (green curve) the peaks of odd-numbered
overtones (no. 1, 3 and so on as counted from left to right) are lower
than the even ones (no. 2, 4 and so on). This is the typical in terms
of physics for springs that are fixed on one side and free on the
other. For all vibrations forming the overtones the fixed end is a
node. The free end is a strong antinode and a weak node, resulting in
the stronger even-numbered overtones. Further explanations are given
in the literature, see bottom of this page.
figure 2
Fundamental note and overtones form the natural harmonic row. The first
overtone vibrates with two times the frequency of the fundamental note,
being its octave (tone B minor in figure 2, under the second grey
triangle). No tone inside this octave can be played on the jew's harp.
The next octave (tone b) again vibrates two times as fast (third
triangle, fourth partial, 58,3 Hz x 4 = 233,2 Hz). Here we have one tone
in between: 3 x 58.3 Hz = 174.9 Hz, which about corresponds to
the tone f with an enharmonic frequency of 174.6 Hz. In the next octave
until b1 (fourth triangle) there are already three overtones. Thus, the
higher we get in the scale, the more tones can be played with a natural
harmonic row.
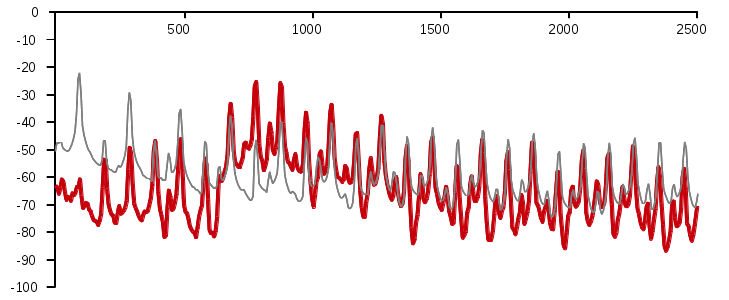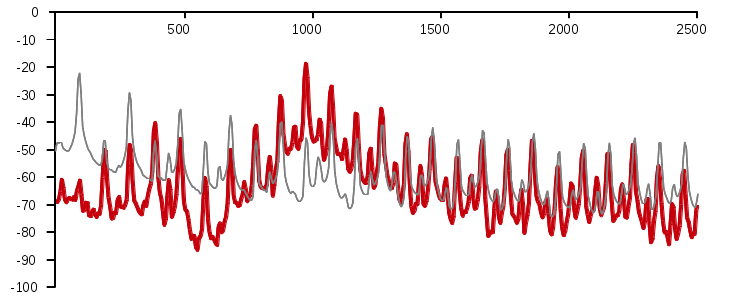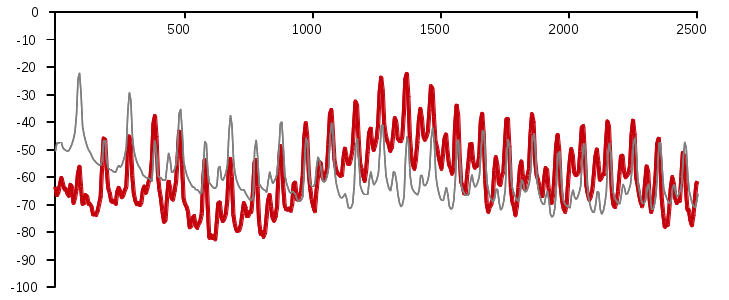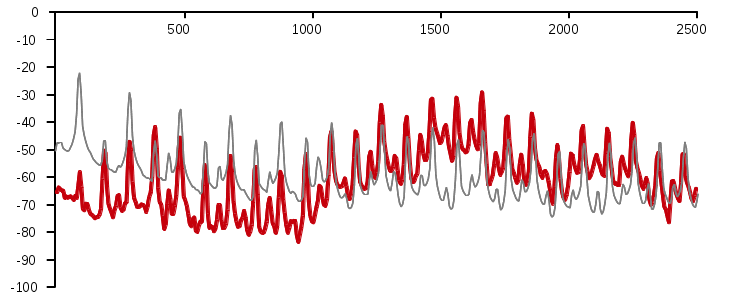
Another example is shown in the animation of figure 3. The grey curve is
the frequency spectrum of a jew's harp tuned G without resonance: The
frame was fixed to a vice, the reed was plucked and the sound recorded.
The red curves show frequency spectra of the same instrument played
normally at the mouth, that is, with resonance. Each curve belongs to
one tone of a tone row played one after the other (sound
example 16, 260 KB) and displayed in the animation
successively. As the playing moves up the tone row, the resonances
of the mouth amplify higher and higher frequencies of the jew's harp
spectrum.
figure 3
(x-axis: frequency, Hz; y-axis: volume, dB)
Robert Vandré, 2016
The overtones of the fundamental note deviate from the tones of the
enharmonic scale. The 10th overtone is almost in the middle
between two tones of the enharmonic scale (see below, figure 5, fourth
peak from the left). These deviations are measured in hundredth of a
half-tone, the so-called cent. As long as the fundamental note is a tone
of the enharmonic scale, the harmonics allways show the same pattern:
For any fundamental note the 10th harmonic will diverge by 49
cent from the enharmonic scale.
Table 1 shows how the tones of the natural harmonic scale (marked dark
grey) fit into the normal (enharmonic) scale. This is a concise overview
of the tones available for playing melodies. A more detailed
overview of the specific scales of all tuned jew's harps is given in the
overtone table (with
explanations, pdf, 68 KB).
table 1
Explanations follow to the right or below.
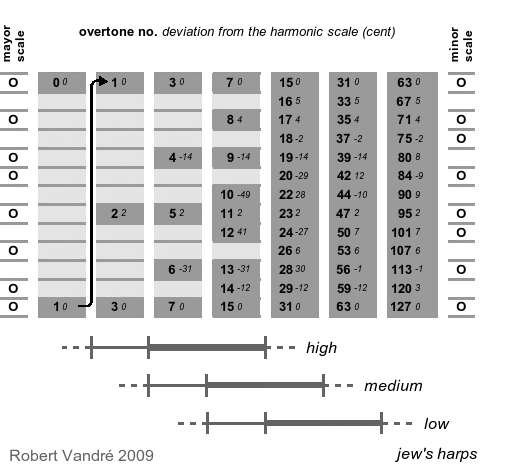 Explanations
Explanations
The enharmonic scale is listed from top left to bottom right,
starting from the fundamental note of the jew's harp. Each
column represents the 12 tones of one octave and the first
note of the following octave. Each row represents a tone and
its octaves.
The fundamental note and its overtones/ harmonics are
marked dark grey.
The bold figures show the number of the overtone. The
small numbers list the deviation of the respective pitch from
the enharminic note as cent. Negative numbers show that the
overtone is below the enharmonic note.
To the left and right of the list of tones circles indicate
the mayor and minor scales respectively, starting from the
fundamental note. Horizontal bars below the table indicate the
tone range playable on different jew's harps. The broad
part of the bar shows the main resonance (second formant, see
below), the narrow part the accompanying lower resonance
(first formant, see below).
On jew's harps with a lower fundamental note more different
pitches can be played than on those with a higher fundamental
note. E.g., a harp tuned A1 plays the
multiplication tables from 55 Hz, wheras a harp tuned G plays
that from 98 Hz. With the multiplication tables from 55 you
will get more steps in the resonance range between 250 and
2000 Hz than with those from 98 Hz.
In sound example 16 (260 kB)
the 9 tones of the 4th octave (4th column of the table) are
played successively on a jew's harp tuned G.
|
Sounds and Pitches, Melodies and Accompaniment |
When playing the jew's harp, it is resonances that produce the
sound: The jew's harp reed vibrates before the mouth. It excites
vibrations of the air column enclosed in the cavities of mouth, throat
and chest. Depending on the shape of the cavities the vibrating air
column enhances certain tones of the natural harmonic row of the jew's
harp. This is shown in figure 2 and 3: Played normally with contact to
the mouth (yellow curve, red curve) the jew's harp has the same tones as
played without contact to the mouth (green curve, grey curve) - the
peaks of both curves are at the same frequencies. But the yellow
and red peaks are higher than the green and grey ones, that is, the
sound is amplified by resonance. Certain frequency regions are
especially amplified by resonance. They are called formants.
Thus, the resonances of the mouth cavity are a filter that amplifies or
reduces the volume of the jew's harp reed at certain frequencies - just
like an equalizer that is a filter for audio signals.
The frequency spectrum of the resonance-"filter" of the mouth can be
illustrated, using one of the tones of the scale shown in figure 3 (cp.
sound example 16 - overtone 11):
The frequency spectrum of the jew's harp without resonance ("vice") was
substracted from the curve of the tone played at the mouth (figure 4,
top). The resulting differential curve shows the amplifying and muffling
effect of the mouth cavern. In the region of 1200 Hz the formant is
displayed as a mountain. Accordingly, this is the frequency of the tone
pitch played. The filter can also be made audible: With the same
position of lips, mouth and tongue, but without jew's harp, the corner
of the mouth was knocked gently by the hand. The frequency spectrum of
this sound resembles that of the
differential curve (figure 4, bottom). Again there is the
formant-mountain around 1200 Hz.
figure 5
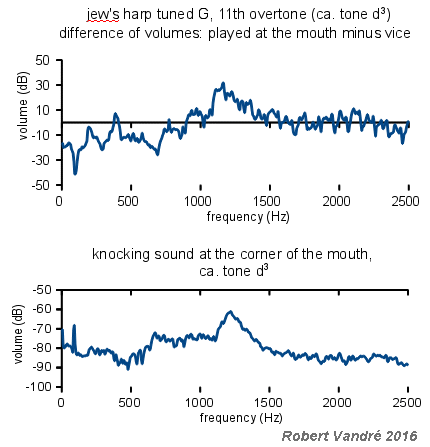
Conclusion: The tones of a certain
jew's harp are unalterable, yet the sounds are many and diverse,
reacting on the slightest changes of resonance in the mouth, e.g. by
movements of the tongue.
Several formants can be active
at the same time. This is illustrated by another small sound experiment
using a jew's harp tuned C (sound
example 17, 70 KB): The reed is plucked regularly 12 times. The
first four strokes I play the tone e3 and the accompanying lower tone g1
(figure 4, green curve). As this jew's harp is tuned C, g1 is the fifth
harmonic (see table 1). At the following four strokes the tones e and g
are switched: I play g3, accompanied by e1 (figure 5, red curve). e1 is
the fourth harmonic of this jew's harp. The last four strokes I play
'openly', like forming the vowel a in "father" (not included in figure
5). Figure 3 shows not the whole frequency spectrum, but only the
peak tops. The amplified frequency regions, that is the formants, are
again forming broad peaks with their summits near the pitches I intended
to play. Again the primary peak tops of the two frequency specta, that
is, the plotted dots of both curves, are at the same frequencies.
figure 5
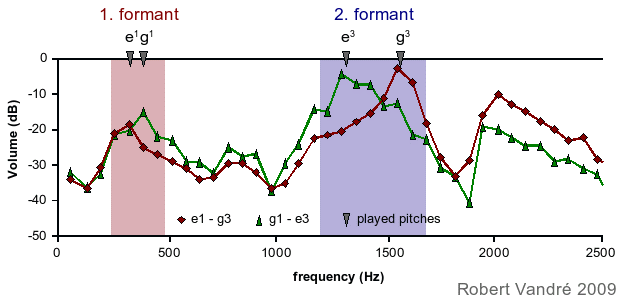
The most pronounced resonance region is the second formant of
the vocal tract, being somewhere in the range from 500 to 2000
Hz. The vocal tract is the sum of the cavities between the voice
and the mouth that form the different linguistic sounds. The highest
peaks of the curves in figure 4 show the second formant (blue background
colour). On the jew's harp, tunes and melodies can be played using the
second formant (see playing techniques: Pitches,
how to play melodies). In addition, the deeper and less pronounced
first formantof the vocal tract can be used to produce
accompanying notes. The first formant can be anywhere in the range
between 250 and 1000 Hz. In figure 5 the lower peak on the left side of
both curves (red background colour) show the first formant. In the piece
of music "Kein schöner Land" (see Music) the
first verse is played without, the second one with accompanying notes.
Different resonance cavities and organs are shown in figure 6, left.
Especially the tongue influences the vocal tract and the jew's harp
sound. The second formant is influenced by movements in the throat
(figure 6, right, blue region), the first formant by movements in the
oral cavity (figure 6, right, red region).
The form of the vocal tract determines the resonances and the formants.
Thus, it is movements of the voice box, the tongue, the jaw and the
lips, that form the sound of speech - and of jew's harp playing.
According to the literature, the relations
between the sound and the form of the vocal tract are complex. But there
are two basic principles that can be illustrated with a simple
experiment with bottles. Here, the bottles are a modell for the vocal
tract. The mouth of the bottle represents the mouth of the player.
When you blow over the mouth like with a panpipe, the sound and pitch of
the bottle cavity can be heard. Bottles with the same volume but
different forms have different pitches. Different 1l-plastic bottles
were tried here (figure 7): The pitch is lower when the cavity is
narrowed near the mouth, and equally when the cavity is widened at the
far end. Accordingly, the bulgy bottle with narrow bottleneck (left) has
a deeper sound than the uniformly shaped one (middle). If the cavity is
shortened and the volume is decreased, the pitch rises. Thus, when the
bottle is partly filled with water, the pitch is higher (right).
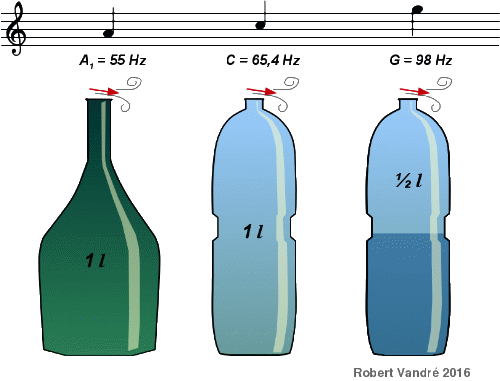
The resonance chambers of mouth and chest of the player can amplifie a
certain range of frequencies, irrespective of the fundamental note of
the jew's harp. This range of tones that can be played is certainly
different for each individual player. In her book on the jew's harp,
Regina Plate states that the pitches that can be played range from 500
to 2000 Hz, corresponding to two octaves. In my experience tones with a
frequency of up to about. 2300 Hz can be played. The notes of the first
formant can be as deep as about 250 Hz. On the basis of the fundamental
note, the tones that can be played on a certain jew's harp can be looked
up in the overtone table (with
explanations, pdf, 68 KB).
| Open and Closed Vocal Tract |
When playing the jew's harp with some breathing, the vocal tract
is open at both sides, to the mouth and to the lungs. But when the voice
chink (or glottis) is closed (see Playing Techniques, Sound
Effects), and also when the tongue closes the oral cavity at the
soft palate like when speaking "ng" in the suffix "-ing", the resonance
chamber is open only at the mouth and closed at the other end. With a
"closed" resonance chamber the jew's harp sound is different and shows
the following peculiarity: The even-numbered overtones (that is, the
tones with even numbers in table 1, see above) are amplified and can be
played especially clearly, but the odd-numbered overtones are not. With
"open" resonance chambers, also tones with odd numberes can be played
clearly. For example, in traditional Norwegian jew's harp playing,
musicians most often open and close the vocal tract for the respective
tones of the scale. This is shown on the following picture from a
workshop held by the Norwegian Jew's Harp Forum (Norsk Munnharpeforum).
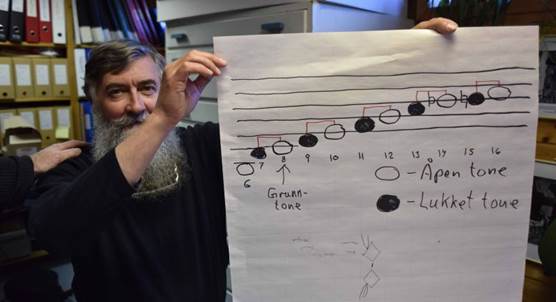
figure 8
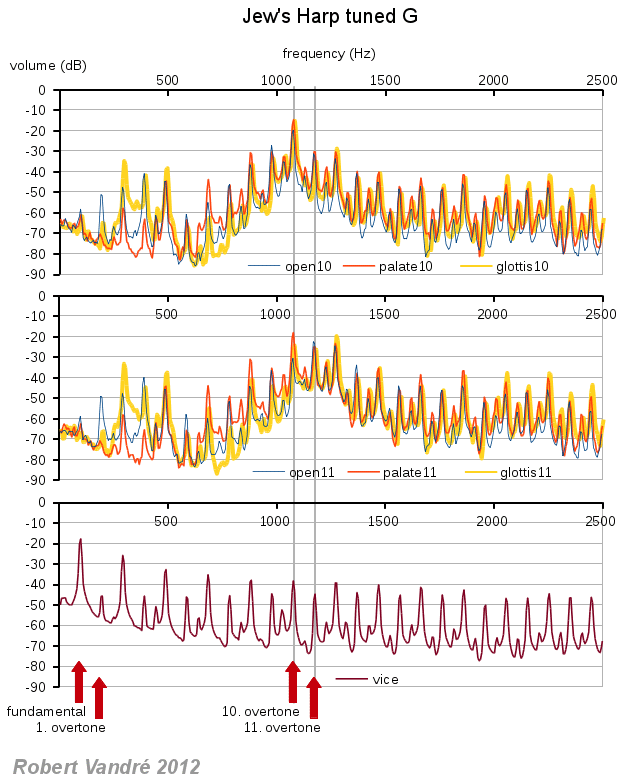
Without resonance (vice), the even numbered overtones are louder than
the odd ones, which is normal for the vibrations of a spring fixed at
one end. When holding the jew's harp to the mouth and intentionally
playing the 10th overtone (about tone cis) the respective peak of the
frequency spectrum is clearly pronounced (figure 4, upper diagramm),
with open as well as closed ("palate", "glottis") modes of playing. With
closed playing, the peak even seems to be a little higher than with open
playing, pronouncing the tone more clearly.
Without resonance, the peak of the11th overtone (tone d) is smaller than
the adjacent 10th and the 12th (lower diagramm, "vice"). When playing
this tone, the respective peak only with open playing is sufficiently
elevated to be at least a little louder than the adjacent ones. Closed
playing pronounces the same frequency region, but the 11th peak is not
elevated over the adjacent ones. Thus, tone d will only be heared with
open playing.
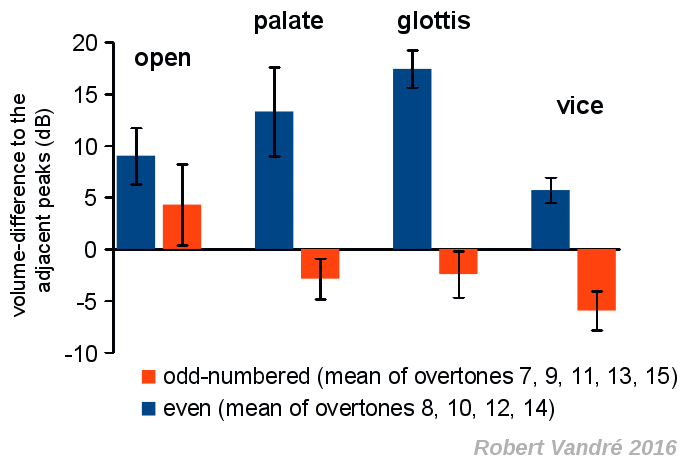
This effect is more clearly shown when all even and odd overtones are
plotted. The volume of the respective played notes (peaks) was compared
to the adjacent peaks. For this purpose the mean dB-value of the
respective two adjacent peaks was substracted from the value of the
central peak. When the resulting difference is positive, the played peak
protrudes from its surroundings - the played tone can be clearly heard.
Figure 9 shows the mean of differences for odd overtones and even
overtones (error bars show standard deviations).
figure 9
That is all. At the end some Music (339 KB).
 Write down
jew's harp music? Sound example "Music" in music notation (27
KB)
Write down
jew's harp music? Sound example "Music" in music notation (27
KB)
| back to playing techniques |
to the contents |
forward to playing on |